软考笔记 - 计算机组成原理
2022年5月左右的预测。
浮点数表示
形似科学计数法,尾数 * 基数(即2) ^ 阶码。一般尾数用补码,阶码用移码。
运算过程先对阶,指调整阶码为相同的,小数向大数看齐;计算尾数;结果格式化,指调整尾数为0.5~1.0之间。
如果题目给定了表示的位数,则应该先确定阶码的大小范围,通过排除快速选出选项。
Flynn分类法
一种根据指令和数据流来对计算平台分类的方法,由Flynn在1972年提出。
| 体系结构类型 | 结构 | 代表 |
|---|---|---|
| SISD | 单控制器;单处理器;单主存 | 单处理器系统 |
| SIMD | 单控制器;多处理器;多主存 | GPU,并行处理机,阵列处理机,超级向量处理机 |
| MISD | 多控制器;单处理器;多主存 | 文献中:流水线计算机 |
| MIMD | 全是多个 | 多核处理器(SMP,BMP,MP),多处理机系统(MPP),多计算机 |
CISC与RISC
- CISC: Complex Instruction Set Computer
- RISC: Reduced Instruction Set Computer
| 指令系统类型 | 指令 | 寻址方式 | 实现方式 |
|---|---|---|---|
| CISC | 数量多,可变长,使用频率差别大 | 支持多种 | 微程序控制技术(微码) |
| RISC | 数量少,定长,使用频率接近; 大部分为单周期指令,通过load/store操作内存 | 支持方式少 | 增加了通用寄存器,硬布线逻辑控制 |
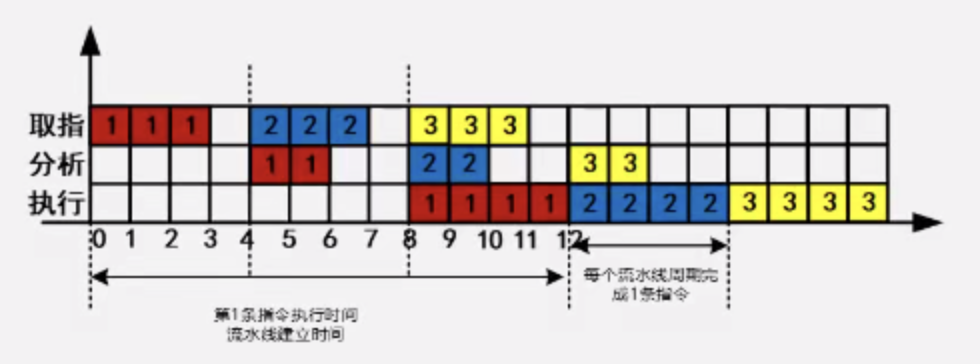
流水线
流水线总时间
流水线的时间计算:1条指令的执行时间 + (指令条数 - 1) * 流水线周期
理论公式:
\[(t_1+t_2+\cdots+t_n) + (n-1) * \Delta_t\]其中$t_1,t_2,\dots,t_n$是一个周期中,每一段的时间。其中流水线周期就是$\max(t_1,t_2,\dots t_n)$,即耗时最长的一个周期中的小段时间,就是流水线周期。
实践公式:
\[t*k+(n-1)*\Delta_t\]该公式平均处理了一个周期中每一小段的时间。此时$k $代表一个周期中有多少个小段,$t$仍然应该是流水线周期,也即是耗时最长的小周期时间。
流水线吞吐率
流水线的吞吐率是指在单位时间内,流水线所完成的实际任务数量或输出的任务数量。基本公式(Through Put Rate):
\[R=\frac{指令条数}{流水线总时间}\]流水线最大吞吐率:
\[R_{max}=\lim_{n\rightarrow\infty}\frac{n}{k*t+(n-1)*t}=\frac{1}{t}\]流水线加速比
定义:完成同样一批任务,不使用流水线所耗时间与使用流水线所耗时间之比。即
\[S=\frac{不使用流水线所耗时间}{使用流水线所耗时间}\]超标量流水线
考点在并行。度为$n$的超标量流水线意味着可以同时进行$n$条指令。如果是度为3,执行100条指令,那么总耗时应该是$[\frac{100}{3}]$,即34条指令 。
计算机组成
CPU组成
运算器
- 算术逻辑单元(Arithmetic logic unit,ALU):算术与逻辑运算
- 累加寄存器AC(Accumulator,AC):通用寄存器,为ALU暂存数据
- 数据缓冲寄存器(Data Register,DR):写内存时暂存
- 状态条件寄存器/条件状态字(Program Status Word, PSW):记录状态与控制标志
控制器
- 程序计数器PC(Program Counter,PC):存储下一条要执行指令的地址
- 指令寄存器IR(Instruction Register,IR):存储即将执行的指令
- 指令译码器ID(Instruction Decoder,ID):对指令中的操作码字段进行分析解释
- 时序部件:提供时序控制信号
冯诺伊曼结构与哈佛结构
冯诺伊曼结构是将指令存储器和数据存储器合并在一起的存储器结构,常见于PC,指令与数据都通过相同的数据总线传输。
哈佛结构是将指令存储和数据存储分开的存储结构,每个存储器独立编址、独立访问,有较高的数据吞吐率。一般用于嵌入式系统中的处理器。有四条总线:指令的数据与地址总线,数据的数据与地址总线。
一些嵌入式芯片
- DSP:实时快速的信号处理固定算法;(典型的哈佛结构)
- SoC:片上系统,集成了CPU和一些其他芯片;
- MPU:微处理器,起控制作用;
- MCU:微控制单元,单片机。包括CPU和一定的外设。
存储结构
速度从快到慢:CPU寄存器、Cache(内容与位置相关)、内存(主存)、外存(辅存)。内存与外存统称虚拟存储系统。除CPU寄存器以外的,称之为三级存储结构。只有Cache不能直接操作,汇编语言可以操作寄存器。
Cache
提高CPU数据IO效率,突破冯诺伊曼瓶颈,即提升CPU与存储系统间的数据传送速率。Cache对程序员来说是透明的。使用Cache改善系统性能依据的是程序的局部性原理。
- 时间局部性:最近访问的指令可能在短期内再次执行(如循环)。
- 空间局部性:一旦访问了某个存储单元,附近的存储单元也可能被访问(顺序执行)。
- 工作集:工作集是进程运行时被频繁访问的页面集合。
Cache的命中率与访问效率
如果以$h$代表Cache访问命中率,$t_1$代表Cache的周期时间,$t_2$代表主存储器周期时间,以读操作为例,使用Cache+主存的平均周期为$t_3$,则有:
\[t_3=h*t_1+(1-h)*t_2\]其中$(1-h)$又称为失效率(未命中率)。
访问效率(设$r=\frac{t_2}{t_1}$):
\[e=\frac{t_1}{t_3}=\frac{t_1}{h*t_1+(1-h)*t_2}=\frac{1}{h+(1-h)*r}=\frac{1}{r+(1-r)h}\]即访问效率仅与命中率相关。替换算法的时间复杂度不影响命中率,替换算法时间复杂度仅影响时间效率。
Cache映像方式
Cache与主存的映像方式:
- 直接相联映像:将主存划分成Cache大小的区块,每个区块的第$n$区域在Cache上的也只能出现在第$n$区域。硬件电路简单,冲突率高。
- 全相联映像:电路难以设计和实现,只适用于小容量Cache,冲突率低。
- 组相联映像:Cache与主存分组对应,直接相联;一组内部的块采用全相联。
Cache页面淘汰
Cache淘汰算法:FIFO先进先出、LRU近期最久未使用、LFU最不经常使用(计数器)、RAND随机。
Cache读写:
- 写直达:同时写Cache与内存
- 写回:只写Cache,淘汰页面再写回内存
- 标记法:只写入内存,并将标志位清0,若用到此数据,再次从内存读取
主存编址
1Byte = 8bit
存储单元个数=最大地址-最小地址+1
按字编址:最小寻址单位为字,如16位、32位、64位bit等;按字节编址:最小寻址单位为一个字节,即8bit。
\[总容量=存储单元个数 * 编址大小单位\] \[总片数=总容量 / 每片的容量\]此类题目中的“8K*4bit”,这里的K,直接用2^10代替。
磁盘管理
磁盘的存储分为磁道(同心圆圈)和扇区(扇形)。磁盘的存取时间由寻道时间和等待时间两部分组成,寻道时间指磁头移动到目标磁道所需的时间,等待时间为等待读写的扇区转到磁头下方所用的时间。
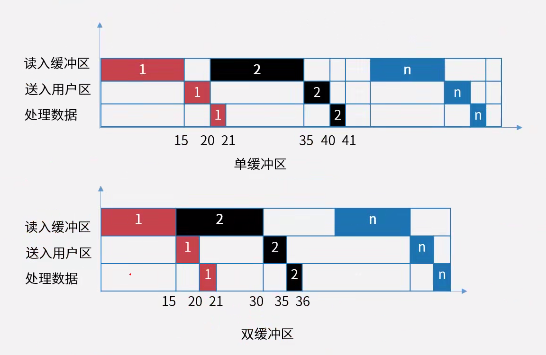
关于磁盘存储块优化的题目,若一开始比较懵圈,建议画一个磁盘圆圈图,再配合题干理解。关于单双缓冲区的题目,也已画图为主,不过也可以结合流水线思路来解题。
如图所示,这样来理解缓冲区问题会明晰很多。
磁盘移臂调度
磁头移动的常见算法:先来先服务FCFS,最短寻道时间优先SSTF,扫描算法SCAN(电梯算法),循环扫描算法CSCAN。
总线
总线是一组能为多个部件分时共享的公共消息传送线路。共享指同一电路。分时指同一时刻仅允许一个点部件向总线发送信息,但允许多个部件同时从总线上接收相同的信息。串行总线适合长距离传输,并行总线适合短距离链接。单工总线:仅能接收或发送;全双工总线:既能接收也能发送;半双工总线:需要切换接收和发送。
总线的分类:
- 数据总线(Data Bus, DB):在CPU与RAM之间传输需要处理、需要存储的数据
- 地址总线(Address Bus, AB):用来指定在RAM之中存储的数据的地址
- 控制总线(Control Bus, CB):将微处理器控制单元的信号,传送到周边设备
总线宽度:32位的总线宽度支持4GB的内存(2^32B=4GB)总线带宽:总线宽度 * 总线频率(可以在使用过程中改变的)
总线的数据发送和接收可以以软件查询方式工作,也可以以中断方式工作。总线按位(bit)传输数据,其数据的正确性依赖校验码纠正。
校验码
| 校验方式 | 校验码位数 | 校验码位置 | 检错 | 纠错 | 校验方式 |
|---|---|---|---|---|---|
| 奇偶校验 | 1 | 一般拼接在头部 | 可检奇数位 错误 | 不可 | 奇校验:奇数个1 |
| CRC循环冗余校验 | 由生成多项式的 最高次幂决定 | 拼接在尾部 | 可检错 | 不可 | 模2除法求余数, 拼接为校验位 |
| 海明校验 | $2^r\ge m+r+1$ | 插入信息中间 | 可检错 | 可纠错 | 分组奇偶校验 |
奇偶校验
由若干位有效信息,再加上一个二进制位(校验位)组成校验码。仅能检查1位(或奇数位)的错误,不可纠错。
- 奇校验:整个校验码,有效信息加上校验位,中的“1”的个数为奇数。
- 偶校验:整个校验码,有效信息加上校验位,中的“1”的个数为偶数。
CRC循环冗余校验
CRC校验可以检查错误(不控制错位个数),不可纠错。把接收到的CRC码用约定的生成多项式$G(x)$去除(模2除法),如果正确,则余数为0;如果某一位出错,则余数不为零。不同的位数出错,其余数也不同,余数和错位序号之间,有一定的对应关系。CRC的校验除数一般在实际中是根据标准而固定的,即有一定的生成多项式。下面以一个例子作为说明。
设生成多项式为$G(x)=x^4+x^3+1$,求二进制序列10110011的校验码。
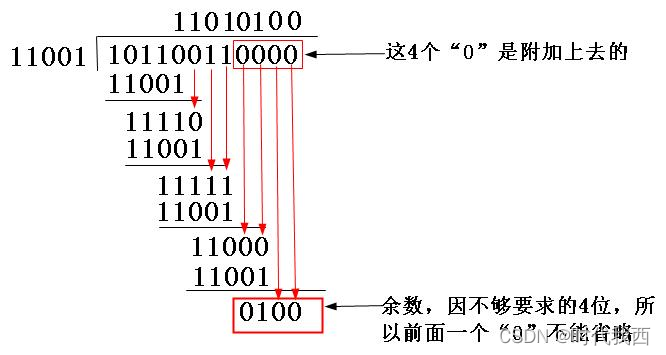
二进制除数总位数是生成多项式最高次幂加一,多项式列出不为零的位数。即二进制比特串为11001。CRC校验码位数是除数减一,即4位。我们在原数据10110011后面补四个0。将补0的二进制序列与除数作模二除法,有如下:
把上步计算得到的CRC校验码0100替换原始数据101100110000后面的四个“0”,得到新数据101100110100,这串新数据发给接收端,接收端做生成多项式二进制为除数的除法,若余数为零,则数据正确无误。
海明校验
设信息位数为$m$,则海明校验码位数$r$需要满足$2^r\ge m+r+1$。假设校验码位数为5,则校验码位置插入在第$2^0,2^1,2^2,2^3.2^4$的位置。海明校验码可以查处错误并纠错。
码制
以八位字长的计算机存储为例。
- 原码:最高位是符号位,其余低位表示数值的绝对值。
- 反码:正数的反码与原码一致,负数的反码符号位不变,其余按位取反。
- 补码:正数的补码与原码一致,负数的补码是其反码末位加一。
- 移码:无论正负数,将其补码的符号位取反即可。
| 码制 | 数值1 | 数值-1 |
|---|---|---|
| 原码 | 0000 0001 | 1000 0001 |
| 反码 | 0000 0001 | 1111 1110 |
| 补码 | 0000 0001 | 1111 1111 |
| 移码 | 1000 0001 | 0111 1111 |
计算机内部的数值计算用补码进行,如上所示,仅补码的$1+(-1)=0$。
如果浮点数的阶码(包括1位阶符)用$R$位的移码表示,尾数(包括1位数符)用$M$位的补码表示,则这种浮点数所能表示的数值范围如下:
- 最大的正数:$(1-2^{-M+1})\times 2^{(2^{R-1}-1)}$
- 最小的负数:$-1\times 2^{(2^{R-1}-1)}$
一些额外补充
AD芯片,即模拟电压信号转数字信号的芯片。一个16位的+5~-5V电压范围的AD芯片的分辨率为:
\[10 \div (2^{16} - 1) = 0.00015259\]总线仲裁机制:菊花链、计数器定时查询、独立请求。其中,菊花链机制跟设备的连接拓扑有关,不能做到各个设备间机会均等。
多核操作系统的技术关键:内核结构、Cache设计、核间通信、任务调度、中断处理、同步互斥
在RAM类存储器中采取0xAA、0x55等数字读入再读出自检;ROM类通过累加和校验进行自检。